521. Дан угол, равный \alpha
. На его биссектрисе взята точка K
; P
и M
— проекции K
на стороны угла. На отрезке PM
взята точка A
такая, что KA=a
. Прямая, проходящая через A
перпендикулярно KA
, пересекает стороны угла в точках B
и C
. Найдите площадь треугольника BKC
.
Ответ. a^{2}\ctg\frac{\alpha}{2}
.
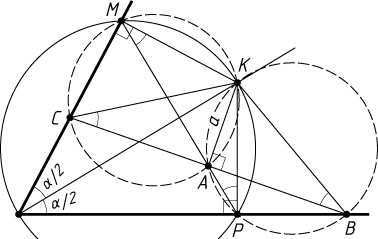
Указание. Точки C
, A
, K
и M
принадлежат одной окружности.
Решение. Заметим, что
\angle PMK=\angle MPK=\frac{\alpha}{2}.
Поскольку отрезок CK
виден из точек A
и M
под прямым углом, то точки C
, A
, K
и M
лежат на одной окружности. Поэтому
\angle ACK=\angle AMK=\frac{\alpha}{2}.
Аналогично
\angle ABK=\angle APK=\frac{\alpha}{2}.
Из прямоугольного треугольника ACK
находим, что
AC=AK\ctg\angle ACK=a\ctg\frac{\alpha}{2}.
Следовательно,
BC=2AC=2a\ctg\frac{\alpha}{2},~S_{\triangle BKC}=\frac{1}{2}BC\cdot AK=a^{2}\ctg\frac{\alpha}{2}.
Источник: Куценок В. Е. Метод вспомогательной окружности: Рукопись. — Киев. — № 25, с. 10
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 13.34, с. 106
