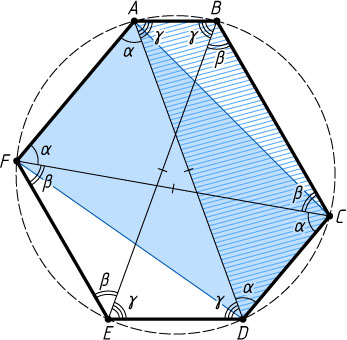
522. В шестиугольнике ABCDEF
известно, что AB\parallel DE
, BC\parallel EF
, CD\parallel FA
и AD=BE=CF
. Докажите, что около этого шестиугольника можно описать окружность.
Указание. Найдите сумму всех внутренних углов данного шестиугольника.
Решение. Поскольку AF\parallel CD
и AD=CF
, то четырёхугольник CDFA
— равнобедренная трапеция или прямоугольник. Поэтому
\angle FCD=\angle ADC=\angle DAF=\angle CFA=\alpha.
Аналогично выводится равенство двух других четвёрок углов. Обозначим их \beta
и \gamma
. Поскольку
4\alpha+4\beta+4\gamma=4\pi
то
\alpha+\beta+\gamma=\pi.
Тогда \angle CDA=\pi-\angle CBA
и точка D
лежит на окружности, проходящей через точки A
, B
и C
. Далее аналогично.
Источник: Московская математическая олимпиада. — 1949, XII, 1-й тур, 9-10 классы
Источник: Гальперин Г. А., Толпыго А. К. Московские математические олимпиады. — М.: Просвещение, 1988. — , № 10, с. 35
Источник: Шклярский Д. О., Ченцов Н. Н., Яглом И. М. Избранные задачи и теоремы элементарной математики. — Ч. 2: Геометрия (планиметрия). — М.: ГТТИ, 1952. — № 109, с. 34
Источник: Белорусская республиканская математическая олимпиада. — 1967, XVII, 8-9 классы