523. Докажите, что площадь описанного многоугольника равна его полупериметру, умноженному на радиус вписанной окружности.
Указание. Соедините центр вписанной окружности с вершинами описанного многоугольника и сложите площади полученных треугольников.
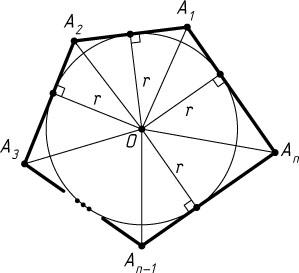
Решение. Соединим центр O
вписанной окружности радиуса r
n
-угольника A_{1}A_{2}\dots A_{n}
с вершинами многоугольника. Тогда
S_{A_{1}A_{2}\dots A_{n}}=S_{\triangle A_{1}OA_{2}}+S_{\triangle A_{2}OA_{3}}+\dots+S_{\triangle A_{n}OA_{1}}=
=\frac{1}{2}A_{1}A_{2}\cdot r+\frac{1}{2}A_{2}A_{3}\cdot r+\dots+\frac{1}{2}A_{n}A_{1}\cdot r=\frac{A_{1}A_{2}+A_{2}A_{3}+\dots+A_{n}A_{1}}{2}\cdot r=pr,
где p
— полупериметр n
-угольника.
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 3, с. 81
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 3, с. 82
