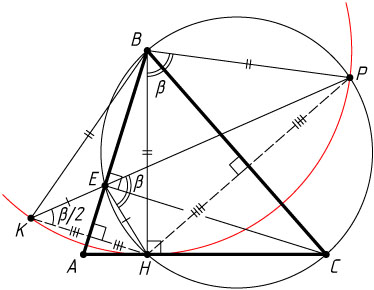
526. Точки K
и P
симметричны основанию H
высоты BH
треугольника ABC
относительно его сторон AB
и BC
. Докажите, что точки пересечения отрезка KP
со сторонами AB
и BC
(или их продолжениями) — основания высот треугольника ABC
.
Указание. Точки K
, H
и P
лежат на окружности с центром в точке B
.
Решение. Пусть E
— точка пересечения KP
и AB
. Точки K
, H
и P
лежат на окружности с центром в точке B
.
Пусть \angle HBP=\beta
. Тогда
\angle HKP=\frac{\beta}{2},~\angle HEP=2\angle HKP=\beta=\angle HBP.
Точки H
и P
лежат на окружности с диаметром BC
, а так как \angle HEP=\angle HBP
, то точка E
также принадлежит этой окружности. Следовательно, \angle BEC=90^{\circ}
, т. е. CE
— высота треугольника ABC
.
Источник: Васильев Н. Б. и др. Математические соревнования. Геометрия. — М.: Наука, 1974. — № 610, с. 14
