527. Через вершину C
квадрата ABCD
проведена прямая, пересекающая диагональ BD
в точке K
, а серединный перпендикуляр к стороне AB
— в точке M
(M
между C
и K
). Найдите \angle DCK
, если \angle AKB=\angle AMB
.
Ответ. 15^{\circ}
.
Указание. Докажите, что треугольник AMB
— равносторонний.
Решение. Поскольку \angle AKB=\angle AMB
, то точки M
, K
, A
и B
лежат на одной окружности. Вписанные в эту окружность углы BKM
и BAM
опираются на одну и ту же дугу, поэтому \angle BKM=\angle BAM
, а так как из симметрии \angle AKB=\angle BKM
, то \angle AMB=\angle BAM
, поэтому MB=AB
. Кроме того, точка M
лежит на серединном перпендикуляре к отрезку AB
, поэтому MA=MB
, значит, треугольник AMB
— равносторонний. Следовательно,
\angle BKM=\angle AMB=60^{\circ},~\angle DCK=\angle BKM-\angle KDC=60^{\circ}-45^{\circ}=15^{\circ}.
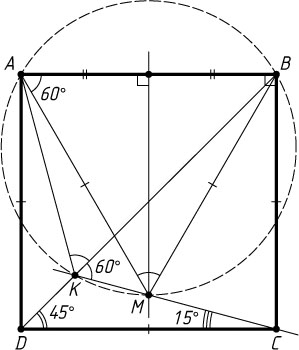
Источник: Куценок В. Е. Метод вспомогательной окружности: Рукопись. — Киев. — № 61, с. 14
Источник: Готман Э. Г. Задачи по планиметрии и методы их решения. — М.: Просвещение, 1996. — № 545, с. 137
