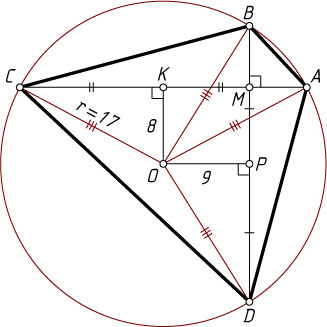
528. В окружность радиуса 17 вписан четырёхугольник, диагонали которого взаимно перпендикулярны и находятся на расстоянии 8 и 9 от центра окружности. Найдите стороны четырёхугольника.
Ответ. \sqrt{848\pm16\sqrt{208}}
, \sqrt{308\pm16\sqrt{208}}
.
Указание. Диаметр, перпендикулярный хорде, делит её пополам.
Решение. Пусть O
— центр окружности, описанной около четырёхугольника ABCD
, M
— точка пересечения диагоналей AC
и BD
, K
— середина AC
, P
— середина BD
, OK=8
, OP=9
. Предположим, что M
находится между P
и B
, а K
— между M
и C
. Тогда
KC=\sqrt{OC^{2}-OK^{2}}=\sqrt{289-64}=15,
DP=\sqrt{OD^{2}-OP^{2}}=\sqrt{208},
MC=CK+KM=CK+OP=15+9=24,
BM=BP-MP=\sqrt{208}-8,
BC=\sqrt{MC^{2}+MB^{2}}=\sqrt{848-16\sqrt{208}}.
Остальные стороны находятся аналогично.
