530. Пусть a
, b
, c
, d
— последовательные стороны четырёхугольника. Докажите, что если S
— его площадь, то S\leqslant\frac{ac+bd}{2}
, причём равенство имеет место тогда и только тогда, когда четырёхугольник вписанный и его диагонали взаимно перпендикулярны.
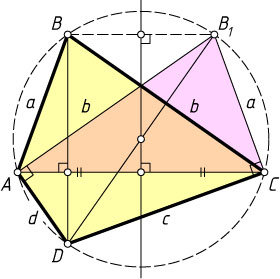
Указание. Пусть ABCD
— данный четырёхугольник. Рассмотрите четырёхугольник AB_{1}CD
, где точка B_{1}
симметрична точке B
относительно серединного перпендикуляра к диагонали AC
.
Решение. Пусть ABCD
— данный четырёхугольник, AB=a
, BC=b
, CD=c
, AD=d
. Рассмотрим четырёхугольник AB_{1}CD
, где точка B_{1}
симметрична вершине B
относительно серединного перпендикуляра к диагонали AC
. Тогда
S_{ABCD}=S_{AB_{1}CD}=\frac{1}{2}CB_{1}\cdot CD\sin\angle B_{1}CD+\frac{1}{2}B_{1}A\cdot AD\sin\angle B_{1}AD\leqslant
\leqslant\frac{1}{2}CB_{1}\cdot CD+\frac{1}{2}B_{1}A\cdot AD=\frac{ac+bd}{2}.
Равенство достигается, если \angle B_{1}CD=\angle B_{1}AD=90^{\circ}
, т. е. четырёхугольник AB_{1}CD
— вписанный, причём его два противоположных угла равны по 90^{\circ}
.
Поскольку диагональ AC
видна из точек B
и B_{1}
под одним углом, то четырёхугольник ABCD
вписан в ту же окружность, а так как AC\parallel BB_{1}
и B_{1}D
— диаметр, то угол между AC
и BD
равен углу B_{1}BD
, т. е. 90^{\circ}
.
Обратно, пусть четырёхугольник ABCD
со сторонами AB=a
, BC=b
, CD=c
, AD=d
вписан в окружность и его диагонали AC
и BD
перпендикулярны. Проведём диаметр DD_{1}
. Тогда
AD_{1}=BC=b,~CD_{1}=AB=a,~\angle DAD_{1}=\angle DCD_{1}=90^{\circ},
S_{ABCD}=S_{ABCD_{1}}=S_{\triangle DAD_{1}}+S_{\triangle DCD_{1}}=\frac{1}{2}AD\cdot AD_{1}+\frac{1}{2}CD\cdot CD_{1}=\frac{ac+bd}{2}.
Примечание. См. также статью М.Горелова «Теорема Птолемея и перекладывание треугольников», Квант, 2017, N1, с.33-35.
Источник: Московская математическая олимпиада. — 1953, XVI, 2-й тур, 8 класс
Источник: Гальперин Г. А., Толпыго А. К. Московские математические олимпиады. — М.: Просвещение, 1988. — № 24, с. 45
Источник: Куценок В. Е. Метод вспомогательной окружности: Рукопись. — Киев. — № 60, с. 17
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 632, с. 80
Источник: Готман Э. Г., Скопец З. А. Решение геометрических задач аналитическим методом: Пособие для учащихся 9—10 кл. — М.: Просвещение, 1979. — № 257(2), с. 40
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 12.18, с. 94
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 17.19, с. 363
