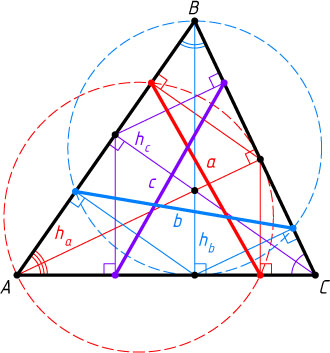
532. Каждое из оснований высот проектируется на две соседние стороны треугольника. Докажите, что длина отрезка, соединяющего эти проекции, не зависит от выбора высоты.
Указание. Докажите, что длина такого отрезка равна соответствующей высоте, умноженной на синус угла, из вершины которого проведена высота.
Решение. Пусть отрезки, соединяющие проекции на две соседние стороны оснований высот h_{a}
, h_{b}
и h_{c}
треугольника ABC
, проведённых из вершин соответственно A
, B
и C
, равны a
, b
и c
соответственно.
Поскольку вершина треугольника, основание соответствующей высоты и проекции основания этой высоты на две соседние стороны треугольника лежат на одной окружности, то по теореме синусов
a=h_{a}\sin\angle A,~b=h_{b}\sin\angle B,
а так как
\frac{h_{a}}{\sin\angle B}=\frac{h_{b}}{\sin\angle A}=AB,
то a=b
. Аналогично a=c
.
Источник: Куценок В. Е. Метод вспомогательной окружности: Рукопись. — Киев. — № 17, с. 9
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 3.10, с. 33
Источник: Готман Э. Г., Скопец З. А. Решение геометрических задач аналитическим методом: Пособие для учащихся 9—10 кл. — М.: Просвещение, 1979. — № 220, с. 36
