537. Хорды AB
, AC
и BC
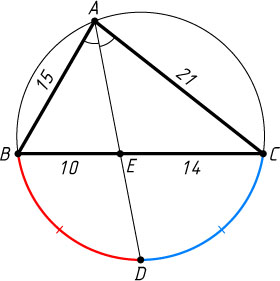
окружности равны соответственно 15, 21 и 24. Точка D
— середина дуги CB
. На какие части BE
и EC
делится хорда BC
прямой AD
?
Ответ. 10 и 14.
Указание. AD
— биссектриса угла BAC
.
Решение. Поскольку точка D
— середина дуги BC
, то \angle DAB=\angle DAC
. Поэтому AE
— биссектриса угла BAC
треугольника BAC
. Следовательно, \frac{BE}{EC}=\frac{AB}{AC}
. Отсюда находим, что
BE=\frac{5}{12}\cdot24=10,~CE=24-10=14.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 25, с. 46
