538. В треугольник вписан полукруг, у которого полуокружность касается основания, а диаметр (с концами на боковых сторонах треугольника) параллелен основанию. Найдите радиус полуокружности, если основание треугольника равно a
, а высота h
.
Ответ. \frac{ah}{a+2h}
.
Указание. Высоты подобных треугольников пропорциональны соответствующим сторонам.
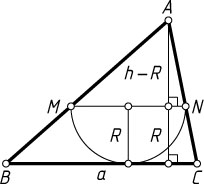
Решение. Пусть M
и N
— концы диаметра полукруга, принадлежащие боковым сторонам AB
и AC
треугольника ABC
с основанием BC=a
и высотой h
, R
— радиус полукруга.
Поскольку треугольники AMN
и ABC
подобны, то
\frac{h-R}{MN}=\frac{h}{BC},~\mbox{или}~\frac{h-R}{2R}=\frac{h}{a}.
Отсюда, находим, что R=\frac{ah}{a+2h}
.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 40, с. 50
