539. Найдите длину хорды, если дан радиус r
окружности и расстояние a
от одного конца хорды до касательной, проведённой через другой её конец.
Ответ. \sqrt{2ar}
.
Указание. Опустите перпендикуляр из центра окружности на данную хорду и рассмотрите образовавшиеся подобные треугольники.
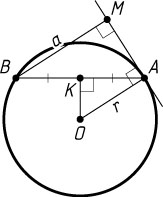
Решение. Пусть O
— центр данной окружности, M
— основание перпендикуляра, опущенного из конца B
хорды AB
на касательную к окружности, проведённую через точку A
, K
— середина AB
.
Поскольку треугольники AKO
и BMA
подобны, то
\frac{AK}{AO}=\frac{MB}{AB},~\mbox{или}~\frac{AB}{2r}=\frac{a}{AB}.
Следовательно, AB=\sqrt{2ar}
.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 45, с. 51
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 8.22, с. 62
