542. Радиус сектора равен r
, а хорда его дуги равна a
. Найдите радиус окружности, вписанной в этот сектор.
Ответ. \frac{ar}{a+2r}
.
Указание. Рассмотрите подобные треугольники.
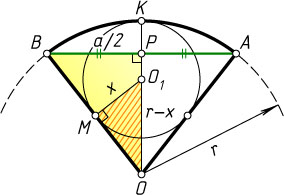
Решение. Пусть OAB
— данный сектор, AB=a
, OA=OB=r
, O_{1}
— центр вписанной в него окружности радиуса x
, K
— точка касания с дугой AB
, M
— точка касания с отрезком OB
, P
— середина AB
. Тогда треугольники OMO_{1}
и OPB
подобны. Поэтому \frac{OO_{1}}{MO_{1}}=\frac{OB}{BP}
, или
\frac{OK-O_{1}K}{MO_{1}}=\frac{OB}{\frac{1}{2}AB},~\mbox{или}~\frac{r-x}{x}=\frac{2r}{a}.
Отсюда находим, что x=\frac{ar}{a+2r}
.
