545. Радиусы двух пересекающихся окружностей равны 13 и 15, а общая хорда равна 24. Найдите расстояние между центрами окружностей.
Ответ. 14 или 4.
Решение. Пусть окружность радиуса 13 с центром O_{1}
и окружность радиуса 15 с центром O_{2}
пересекаются в точках A
и B
. Точки O_{1}
и O_{2}
равноудалены от концов отрезка AB
, поэтому прямая O_{1}O_{2}
— серединный перпендикуляр к отрезку AB
.
Пусть M
— середина AB
. Из прямоугольных треугольников AMO_{1}
и AMO_{2}
по теореме Пифагора находим, что
MO_{1}=\sqrt{13^{2}-12^{2}}=5,~MO_{2}=\sqrt{15^{2}-12^{2}}=9.
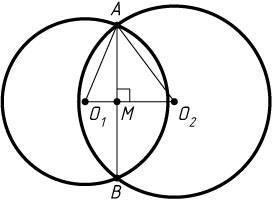
Если точки O_{1}
и O_{2}
лежат по разные стороны от прямой AB
(рис. 1), то
O_{1}O_{2}=MO_{1}+MO_{2}=5+9=14.
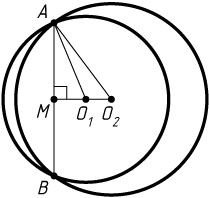
Если же точки O_{1}
и O_{2}
лежат по одну сторону от прямой AB
(рис. 2), то
O_{1}O_{2}=MO_{2}-MO_{1}=9-5=4.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 33(3), с. 57
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — с. 74

