546. AB
и CD
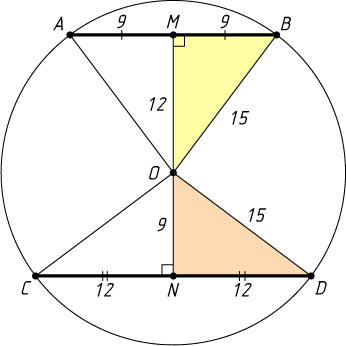
— две параллельные хорды, расположенные по разные стороны от центра O
окружности радиуса 15. AB=18
, CD=24
. Найдите расстояние между хордами.
Ответ. 21.
Указание. Диаметр, перпендикулярный хорде, делит её пополам.
Решение. Через центр O
окружности проведём диаметр, перпендикулярный данным хордам. Он пересекает хорды в их серединах: M
(AB)
и N
(CD)
. Искомое расстояние:
MN=OM+ON=\sqrt{OB^{2}-MB^{2}}+\sqrt{OD^{2}-DN^{2}}=12+9=21.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 33(4), с. 57
