549. Радиус окружности равен 25; две параллельные хорды равны 14 и 40. Найдите расстояние между ними.
Ответ. 39 или 9.
Указание. Рассмотрите два случая взаимного расположения хорд.
Решение. Расстояния от центра окружности до данных хорд равны
\sqrt{25^{2}-20^{2}}=15,~\sqrt{25^{2}-7^{2}}=24.
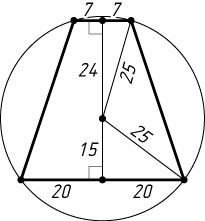
Если хорды расположены по разные стороны от центра (рис. 1), то расстояние между ними равно 24+15=39
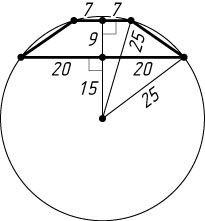
, а если по одну (рис. 2), — то 24-15=9
.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 36, с. 57
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 4.5, с. 30

