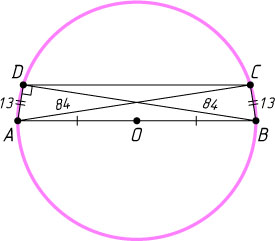
550. Расстояния от одного конца диаметра до концов параллельной ему хорды равны 13 и 84. Найдите радиус окружности.
Ответ. 42,5.
Указание. Диагонали равнобедренной трапеции равны.
Решение. Пусть AB
— данный диаметр, CD
— данная хорда, AD=13,AC=84
. Трапеция ABCD
— равнобедренная, поэтому BD=AC=84
.
Из прямоугольного треугольника ADB
находим, что
AB=\sqrt{AD^{2}+DB^{2}}=\sqrt{13^{2}+84^{2}}=\sqrt{169+7056}=\sqrt{7225}=85.
Следовательно, радиус равен 42,5.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 37, с. 57
