554. Две окружности радиусов r
и R
касаются внешним образом. Из центра одной окружности проведена касательная к другой, а из полученной точки касания проведена касательная к первой окружности. Найдите длину последней касательной.
Ответ. \sqrt{2rR}
.
Указание. Линия центров двух касающихся окружностей проходит через их точку касания.
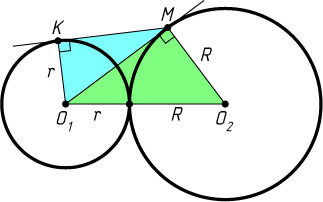
Решение. Пусть O_{1}
и O_{2}
— центры окружностей, M
и K
— первая и вторая точки касания на окружностях с центрами O_{2}
и O_{1}
соответственно.
Из прямоугольного треугольника MO_{1}O_{2}
находим, что
O_{1}M=\sqrt{O_{1}O_{2}^{2}-MO_{2}^{2}}=\sqrt{(R+r)^{2}-R^{2}}=\sqrt{r^{2}+2rR}.
Из прямоугольного треугольника MKO_{1}
находим, что
MK=\sqrt{MO_{1}^{2}-KO_{1}^{2}}=\sqrt{r^{2}+2rR-r^{2}}=\sqrt{2rR}.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 39, с. 58
