555. Две окружности касаются внешним образом. Найдите длину их общей внешней касательной (между точками касания), если радиусы равны 16 и 25.
Ответ. 40.
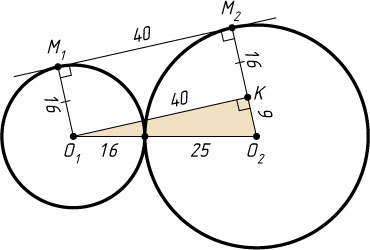
Указание. Опустите перпендикуляр из центра меньшей окружности на радиус большей, проведённый в точку касания с общей внешней касательной.
Решение. Пусть O_{1}
и O_{2}
— центры данных окружностей, M_{1}
и M_{2}
— точки их касания с общей внешней касательной, K
— основание перпендикуляра, опущенного из точки O_{1}
на O_{2}M_{2}
. В прямоугольном треугольнике O_{1}KO_{2}
известно, что
KO_{1}=\sqrt{O_{1}O_{2}^{2}-KO_{2}^{2}}=\sqrt{(16+25)^{2}-(25-16)^{2}}=
=\sqrt{4\cdot16\cdot25}=2\cdot4\cdot5=40.
Следовательно, M_{1}M_{2}=KO_{1}=40
.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 40(1), с. 58
