556. Радиусы двух окружностей равны 27 и 13, а расстояние между центрами равно 50. Найдите длины их общих касательных.
Ответ. 48 и 30.
Указание. Рассмотрите случаи общей внешней и общей внутренней касательных.
Решение. Пусть O_{1}
— центр окружности радиуса 27, O_{2}
— центр окружности радиуса 13, A
и B
соответственно — точки касания окружностей с их общей внешней касательной, C
и D
соответственно — с внутренней, P
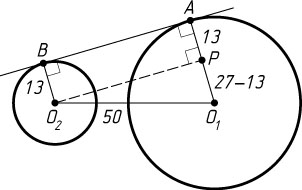
— основание перпендикуляра, опущенного из O_{2}
на O_{1}A
(рис. 1). Из прямоугольного треугольника O_{1}O_{2}P
находим, что
O_{2}P=\sqrt{O_{1}O^{2}_{2}-O_{1}P^{2}}=\sqrt{50^{2}-(27-13)^{2}}=48,
а так как APO_{2}B
— прямоугольник, то AB=O_{2}P=48
.
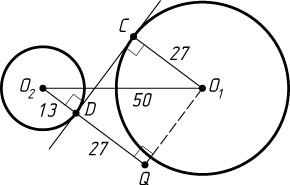
Пусть Q
— основание перпендикуляра, опущенного из O_{1}
на продолжение радиуса O_{2}D
(рис. 2). Тогда
O_{1}Q=\sqrt{O_{1}O^{2}_{2}-O_{2}Q^{2}}=\sqrt{50^{2}-(27+13)^{2}}=30,
а так как DQO_{1}C
— прямоугольник, то CD=O_{1}Q=30
.
