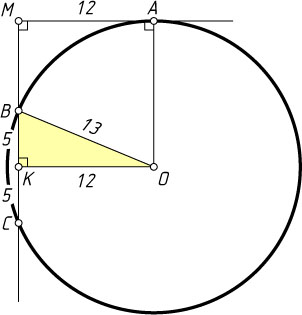
557. Касательная и секущая, проведённые из одной точки к окружности, взаимно перпендикулярны. Касательная равна 12, а внутренняя часть секущей равна 10. Найдите радиус окружности.
Ответ. 13.
Указание. Расстояние от центра окружности до секущей равно данному отрезку касательной.
Решение. Пусть O
— центр окружности, M
— общая точка касательной и секущей, A
— точка касания, BC
— внутренняя часть секущей MC
, K
— середина BC
. Тогда OK\perp BC
и
OB^{2}=OK^{2}+BK^{2}=AM^{2}+BK^{2}=144+25=169.
Следовательно, OB=13
.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 41, с. 58
