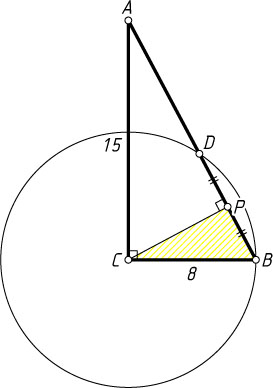
558. Катеты AC
и CB
прямоугольного треугольника ABC
равны 15 и 8 соответственно. Из центра C
радиусом CB
описана дуга, отсекающая от гипотенузы часть BD
. Найдите BD
.
Ответ. \frac{128}{17}
.
Указание. Перпендикуляр, опущенный из точки C
на AB
, проходит через середину BD
.
Решение. Опустим перпендикуляр CP
на хорду BD
. Тогда P
— середина BD
. Поскольку BC\cdot AC=AB\cdot CP
, то CP=\frac{120}{17}
. Из прямоугольного треугольника CPB
находим, что
PB^{2}=BC^{2}-CP^{2}=\frac{64}{17}
Следовательно, BD=2PB=\frac{128}{17}
.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 44, с. 58
