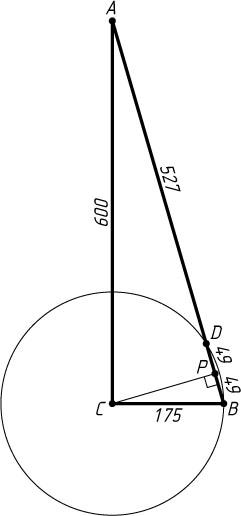
559. Окружность с центром в вершине прямого угла прямоугольного треугольника радиуса, равного меньшему катету, делит гипотенузу на отрезки в 98 и 527 (начиная от меньшего катета). Найдите катеты.
Ответ. 175 и 600.
Указание. Примените теорему о высоте прямоугольного треугольника, опущенной на гипотенузу.
Решение. Пусть C
— вершина прямого угла, BC
— меньший катет, D
— точка данной окружности, лежащая на гипотенузе AB
, BD=98
, AD=527
.
Пусть P
— основание перпендикуляра, опущенного из точки C
на AB
. Тогда
BC^{2}=BP\cdot AB=49(527+98)=49\cdot625.
Поэтому
BC=7\cdot25=175,~AC^{2}=AP\cdot AB=576\cdot625.
Следовательно, AC=600
.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 45, с. 58
