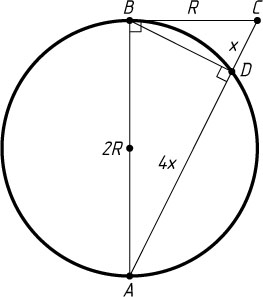
561. AB
— диаметр окружности, BC
и CDA
— касательная и секущая. Найдите отношение CD:DA
, если BC
равно радиусу окружности.
Ответ. 1:4
.
Указание. Примените теорему о высоте прямоугольного треугольника, проведённой из вершины прямого угла.
Решение. Обозначим через R
радиус окружности. Тогда BC=R
, AB=2R
. Поскольку
AB^{2}=AD\cdot AC,~BC^{2}=AC\cdot CD,
то
DC=\frac{4R^{2}}{AC},~AD=\frac{R^{2}}{AC}.
Следовательно, CD:DA=1:4
.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 47, с. 58
