564. Радиус окружности равен R
. Найдите хорду, проведённую из конца данного диаметра через середину перпендикулярного к нему радиуса.
Ответ. \frac{4R\sqrt{5}}{5}
.
Указание. Вписанный угол, опирающийся на диаметр, — прямой.
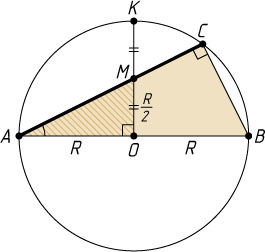
Решение. Пусть AB
— диаметр, OK
— перпендикулярный ему радиус, AC
— хорда, проходящая через середину M
радиуса OK
.
Поскольку \angle ACB=90^{\circ}
, то треугольники AOM
и ACB
подобны. Следовательно, \frac{AC}{AB}=\frac{AO}{AM}
. AM
найдём по теореме Пифагора из треугольника AOM
(AO=R
, OM=\frac{R}{2}
).
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 58(2), с. 60
