565. В прямоугольном треугольнике ABC
катет AC
равен 16 и катет BC
равен 12. Из центра B
радиусом BC
описана окружность и к ней проведена касательная, параллельная гипотенузе (причём касательная и треугольник лежат по разные стороны от гипотенузы). Катет BC
продолжен до пересечения с проведённой касательной. Определите, на сколько продолжен катет.
Ответ. 15.
Указание. Рассмотрите подобные треугольники.
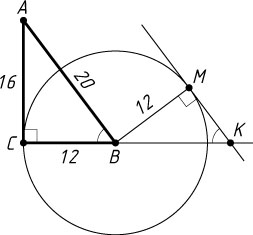
Решение. Пусть M
— точка касания, K
— точка пересечения касательной с продолжением катета CB
.
AB^{2}=CB^{2}+CA^{2}=144+256=400,~AB=20.
Треугольники BMK
и ACB
подобны, поэтому \frac{BK}{BM}=\frac{AB}{AC}
. Следовательно, BK=\frac{20\cdot12}{16}=15
.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 59, с. 60
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 8.18, с. 61
