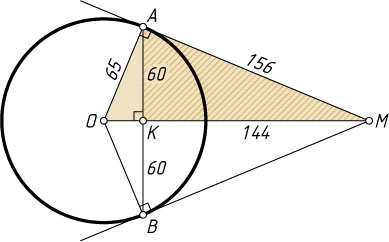
566. Из одной точки проведены к кругу две касательные. Длина касательной равна 156, а расстояние между точками касания равно 120. Найдите радиус круга.
Ответ. 65.
Указание. Рассмотрите подобные треугольники.
Решение. Пусть O
— центр круга, MA
и MB
— касательные, A
и B
— точки касания, K
— середина AB
. Тогда
MK^{2}=AM^{2}-AK^{2}=156^{2}-60^{2}=96\cdot216=144^{2}.
Из подобия треугольников MAO
и MKA
следует, что \frac{OA}{AM}=\frac{AK}{MK}
. Поэтому
OA=\frac{AM\cdot AK}{MK}=\frac{156\cdot60}{144}=65.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 60, с. 60
