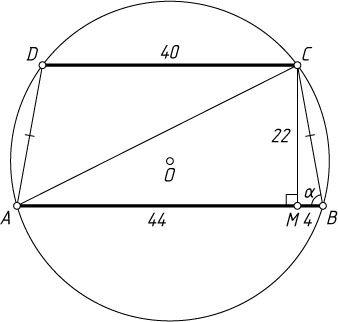
569. Длины двух параллельных хорд окружности равны 40 и 48, расстояние между ними равно 22. Найдите радиус окружности.
Ответ. 25.
Указание. Проведите диагональ полученной трапеции и найдите радиус окружности, описанной около одного из получившихся треугольников.
Решение. Первый способ. Пусть AB=48
и CD=40
— параллельные хорды, причём A
, B
, C
и D
— последовательные вершины равнобедренной трапеции ABCD
, M
— основание перпендикуляра, опущенного из точки C
на AB
. Тогда
AM=44,~BM=4,~AC^{2}=AM^{2}+CM^{2}=44^{2}+22^{2}=(22\sqrt{5})^{2},
BC^{2}=CM^{2}+BM^{2}=(10\sqrt{5})^{2},~\sin\angle ABC=\frac{CM}{BC}=\frac{11}{5\sqrt{5}}.
Если R
— искомый радиус, то
R=\frac{AC}{2\sin\angle ABC}=25.
Второй способ. Обозначим искомый радиус через R
и составим иррациональные уравнения
\sqrt{R^{2}-20^{2}}+\sqrt{R^{2}-24^{2}}=22
для случая, когда центр окружности лежит между хордами, и
\sqrt{R^{2}-20^{2}}-\sqrt{R^{2}-24^{2}}=22,
— если вне. Первое уравнение имеет единственное положительное решение R=25
. Второе уравнение решений не имеет.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 69, с. 61
