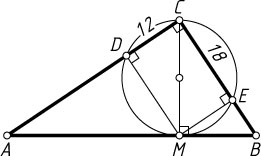
573. В прямоугольном треугольнике проведена высота из вершины прямого угла. На этой высоте как на диаметре построена окружность. Известно, что эта окружность высекает на катетах отрезки, равные 12 и 18. Найдите катеты.
Ответ. 39 и 26.
Указание. Соедините концы указанных отрезков с основаниями перпендикуляра.
Решение. Пусть данная окружность пересекает катеты AC
и BC
треугольника ABC
соответственно в точках D
и E
, отличных от точки C
, причём CD=12
и CE=18
. Если M
— основание перпендикуляра, опущенного из вершины C
на AB
, то
\angle MDC=\angle MEC=90^{\circ},~DM=CE=18,~ME=CD=12.
Из прямоугольных треугольников AMC
и BMC
находим, что
DM^{2}=AD\cdot DC,~ME^{2}=BE\cdot EC.
Значит,
AD=\frac{DM^{2}}{DC}=\frac{18^{2}}{12}=27,~BE=\frac{ME^{2}}{EC}=\frac{12^{2}}{18}=8.
Следовательно,
AC=AD+DC=27+12=39,~BC=BE+EC=8+18=26.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 75, с. 61
