575. Две окружности радиуса r
касаются большей окружности радиуса R
— одна изнутри, другая извне, причём градусная мера дуги между точками касания равна 60^{\circ}
. Найдите расстояние между центрами меньших окружностей.
Ответ. \sqrt{R^{2}+3r^{2}}
.
Указание. Линия центров двух касающихся окружностей проходит через точку касания.
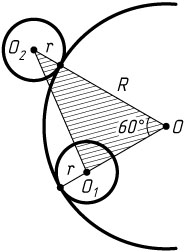
Решение. Пусть O
, O_{1}
и O_{2}
— центры данных окружностей. В треугольнике O_{1}OO_{2}
известно, что
OO_{1}=R-r,~OO_{2}=R+r,~\angle O_{1}OO_{2}=60^{\circ}.
По теореме косинусов
O_{1}O^{2}_{2}=(R+r)^{2}+(R-r)^{2}-2(R+r)(R-r)\cos60^{\circ}=
=R^{2}+3r^{2}.
Источник: Рыбкин Н. А. Сборник задач по геометрии. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1961. — № 101, с. 64
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — с. 64
