592. В трапеции ABCD
с основаниями AD
и BC
боковая сторона AB
равна 2. Биссектриса угла BAD
пересекает прямую BC
в точке E
. В треугольник ABE
вписана окружность, касающаяся стороны AB
в точке M
и стороны BE
в точке H
, MH=1
. Найдите угол BAD
.
Ответ. 120^{\circ}
.
Указание. Обозначьте BM
через x
и воспользуйтесь подобием равносторонних треугольников BMH
и BAE
.
Решение. Поскольку BE
параллельно AD
, то
\angle AEB=\angle EAD=\angle BAE.
Поэтому треугольник ABE
— равнобедренный. Следовательно, BE=AB=2
и MH\parallel AE
.
Обозначим BM=BH=x
. Пусть K
— точка касания данной окружности со стороной AE
. Тогда
AK=AM=AB-BM=2-x,~KE=2-x,~AE=4-2x.
Из подобия равнобедренных треугольников MBH
и ABE
следует, что
\frac{MH}{AE}=\frac{BM}{AB},~\mbox{или}~\frac{1}{4-2x}=\frac{x}{2},~\mbox{или}~x^{2}-2x+1=0.
Отсюда находим, что x=1
, т. е. эти треугольники — равносторонние. Следовательно,
\angle BAD=2\angle BAE=120^{\circ}.
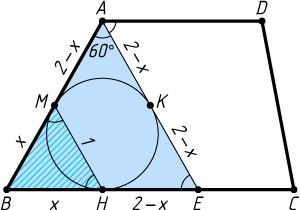
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 41
Источник: Вступительный экзамен на химический факультет МГУ. — 1978, вариант 1, № 4
