594. В параллелограмме ABCD
сторона AD
равна 6. Биссектриса угла ADC
пересекает прямую AB
в точке E
. В треугольник ADE
вписана окружность, касающаяся стороны AE
в точке K
и стороны AD
в точке T
, KT=3
. Найдите угол BAD
.
Ответ. 60^{\circ}
.
Решение. Прямые AE
и CD
параллельны, а DE
— биссектриса угла ADC
, поэтому \angle AED=\angle CDE=\angle ADE
. Значит, треугольник ADE
равнобедренный, AD=AE
.
Пусть окружность касается основания DE
равнобедренного треугольника ADE
в точке M
. Тогда M
— середина DE
. Обозначим DM=x
. Тогда DT=DM=x
, AT=AD-DT=6-x
. Треугольник ATK
подобен треугольнику ADE
, поэтому \frac{AT}{AD}=\frac{TK}{DE}
, или \frac{6-x}{6}=\frac{3}{2x}
. Отсюда находим, что x=3
. Тогда DE=2x=6
, значит, треугольник ADE
равносторонний. Следовательно, \angle BAD=\angle EAD=60^{\circ}
.
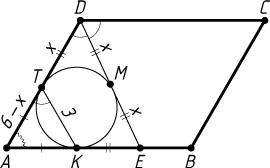
Источник: Вступительный экзамен на химический факультет МГУ. — 1978, вариант 3, № 4
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1983. — с. 53
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 14.39, с. 139
