601. Хорды AB
и AC
равны между собой, угол BAC
равен 30^{\circ}
. Найдите отношение площади той части круга, которая заключена внутри этого угла, к площади всего круга.
Ответ. \frac{\pi+3}{6\pi}
.
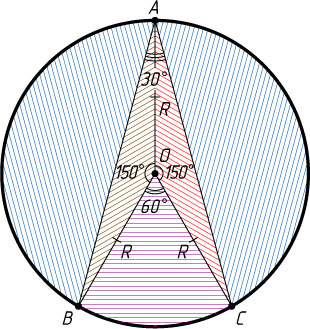
Указание. Часть круга, заключённого в данном угле, состоит из сектора с углом 60^{\circ}
и двух равных равнобедренных треугольников.
Решение. Поскольку треугольник ABC
остроугольный, то центр его описанной окружности расположен внутри треугольника. Пусть O
— центр окружности, R
— её радиус. Часть круга, заключённая в данном угле, состоит из сектора BOC
с углом \angle BOC
, равным 60^{\circ}
, и двух равных равнобедренных треугольников AOB
и AOC
с углами при вершинах, равными \frac{360^{\circ}-60^{\circ}}{2}=150^{\circ}
.
Площадь сектора составляет шестую часть площади круга, т. е. \frac{\pi R^{2}}{6}
, а площадь каждого треугольника равна
\frac{1}{2}R^{2}\sin150^{\circ}=\frac{R^{2}}{4}.
Следовательно, искомое отношение равно
\frac{\frac{\pi R^{2}}{6}+\frac{R^{2}}{2}}{\pi R^{2}}=\frac{\pi+3}{6\pi}.
Источник: Вступительный экзамен на факультет почвоведения МГУ. — 1980, вариант 1, № 3
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 62
