602. На основании равностороннего треугольника как на диаметре построена полуокружность, рассекающая треугольник на две части. Сторона треугольника равна a
. Найдите площадь той части треугольника, которая лежит вне круга.
Ответ. \frac{a^{2}(3\sqrt{3}-\pi)}{24}
.
Указание. Докажите, что указанная полуокружность проходит через середины двух сторон данного треугольника.
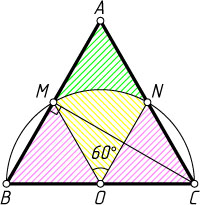
Решение. Пусть полуокружность с центром O
, построенная на стороне BC
равностороннего треугольника ABC
как на диаметре, пересекает его стороны AB
и AC
в точках M
и N
соответственно. Тогда CM
— высота треугольника ABC
. Поэтому M
— середина AB
и треугольник MOB
подобен треугольнику ACB
с коэффициентом \frac{1}{2}
. Следовательно, S_{\triangle MOB}=\frac{1}{4}S_{\triangle ABC}
. Аналогично S_{\triangle NOC}=\frac{1}{4}S_{\triangle ABC}
.
Поскольку \angle MON=60^{\circ}
, то площадь сектора MON
составляет шестую часть площади круга радиуса \frac{a}{2}
, т. е. равна \frac{\pi a^{2}}{24}
. Следовательно, искомая площадь равна
\frac{a^{2}\sqrt{3}}{4}-\frac{a^{2}\sqrt{3}}{8}-\frac{\pi a^{2}}{24}=\frac{a^{2}(3\sqrt{3}-\pi)}{24}.
Источник: Вступительный экзамен на факультет почвоведения МГУ. — 1980, вариант 2, № 3
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 62
