603. Прямая, проходящая через точки A
и B
окружности, рассекает её на две дуги. Длины этих дуг относятся как 1:11
. В каком отношении хорда AB
делит площадь круга, ограниченного данной окружностью?
Ответ. \frac{\pi-3}{11\pi+3}
.
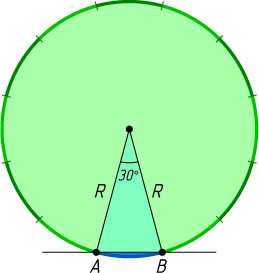
Указание. Площадь меньшего из сегментов равна разности площадей сектора с углом 30^{\circ}
и равнобедренного треугольника.
Решение. Точки A
и B
разбивают окружность на две дуги, меньшая из которых содержит \frac{360^{\circ}}{12}=30^{\circ}
. Площадь соответствующего сегмента равна разности площадей сектора и треугольника, т. е.
\frac{\pi R^{2}}{12}-\frac{R^{2}}{4}=\frac{R^{2}(\pi-3)}{12},
где R
— радиус круга. Тогда площадь оставшегося сегмента равна
\pi R^{2}-\frac{R^{2}(\pi-3)}{12}=\frac{R^{2}(11\pi+3)}{12}.
Следовательно, искомое отношение равно \frac{\pi-3}{11\pi+3}
.
Источник: Вступительный экзамен на факультет почвоведения МГУ. — 1980, вариант 3, № 3
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1983. — с. 79
