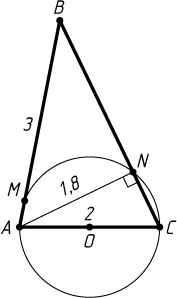
607. В треугольнике ABC
на стороне AC
как на диаметре описана окружность, которая пересекает сторону AB
в точке M
, а сторону BC
в точке N
. Известно, что AC=2
, AB=3
, AN=1{,}8
. Найдите косинус угла BAC
.
Ответ. \arccos(0{,}54-0{,}4\sqrt{0{,}76})
.
Указание. Найдите отрезки BN
и NC
и примените теорему косинусов.
Решение. Из прямоугольных треугольников ANC
и ANB
находим, что
CN=\sqrt{AC^{2}-AN^{2}}=\sqrt{0{,}76},~BN=\sqrt{AB^{2}-AN^{2}}=2{,}4.
Следовательно, BC=2{,}4+\sqrt{0{,}76}
.
По теореме косинусов из треугольника ABC
находим, что
\cos\angle BAC=\frac{AB^{2}+AC^{2}-BC^{2}}{2AB\cdot AC}=\frac{13-(2{,}4+\sqrt{0{,}76})^{2}}{12}=
=0{,}54-0{,}4\sqrt{0{,}76}.
Источник: Вступительный экзамен на географический факультет МГУ. — 1981, вариант 3, № 4
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1983. — с. 92
