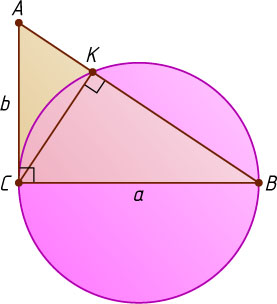
611. На катете BC
прямоугольного треугольника ABC
как на диаметре построена окружность, которая пересекает гипотенузу AB
в точке K
. Найдите площадь треугольника CKB
, если катет BC=a
и AC=b
.
Ответ. \frac{a^{3}b}{2(a^{2}+b^{2})}
.
Решение. По теореме Пифагора
AB=\sqrt{BC^{2}+AC^{2}}=\sqrt{a^{2}+b^{2}}.
Точка K
лежит на окружности с диаметром BC
, поэтому \angle BKC=90^{\circ}
. Треугольник CBK
подобен треугольнику ABC
по двум углам, причём коэффициент подобия равен \frac{BC}{AB}=\frac{a}{\sqrt{a^{2}+b^{2}}}
, значит, площадь треугольника CBK
равна площади треугольника ABC
, умноженной на квадрат коэффициента подобия, т. е.
S_{\triangle CBK}=\left(\frac{a}{\sqrt{a^{2}+b^{2}}}\right)^{2}\cdot\frac{1}{2}ab=\frac{a^{3}b}{2(a^{2}+b^{2})}.
Источник: Вступительный экзамен на географический факультет МГУ. — 1983, вариант 3, № 3
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 75
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 5.13, с. 39
Источник: Шарыгин И. Ф. Факультативный курс по математике. Решение задач: Учебное пособие для 10 кл. — М.: Просвещение, 1989. — № 46, с. 195
