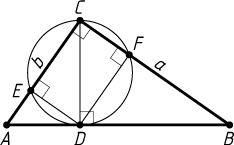
612. На высоте CD
, опущенной из вершины C
прямоугольного треугольника ABC
на гипотенузу AB
, как на диаметре построена окружность, которая пересекает катет AC
в точке E
, а катет BC
в точке F
. Найдите площадь четырёхугольника CFDE
, если катет AC
равен b
, а катет BC
равен a
.
Ответ. \frac{a^{3}b^{3}}{(a^{2}+b^{2})^{2}}
.
Указание. Для нахождения сторон прямоугольника CFDE
воспользуйтесь теоремой о высоте прямоугольного треугольника, проведённой из вершины прямого угла.
Решение. Поскольку 2S_{\triangle ABC}=AB\cdot CD=AC\cdot BC
, то
CD=BC\cdot\frac{AC}{AB}=\frac{ab}{\sqrt{a^{2}+b^{2}}}.
Поскольку DF
— высота прямоугольного треугольника CDB
, проведённая из вершины прямого угла, то
CF=\frac{CD^{2}}{BC}=\frac{ab^{2}}{(a^{2}+b^{2})}.
Аналогично находим, что CE=\frac{a^{2}b}{(a^{2}+b^{2})}
.
Поскольку CFDE
— прямоугольник, то
S_{CFDE}=CF\cdot CE=\frac{a^{3}b^{3}}{(a^{2}+b^{2})^{2}}.
Источник: Вступительный экзамен на географический факультет МГУ. — 1983, вариант 4, № 3
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 76
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 5.14, с. 40
