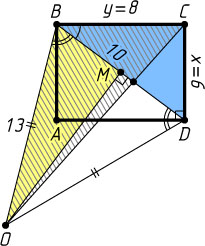
627. Площадь прямоугольника ABCD
равна 48, а диагональ равна 10. На плоскости, в которой расположен прямоугольник, выбрана точка O
, для которой OB=OD=13
. Найдите расстояние от точки O
до наиболее удалённой от неё вершины прямоугольника.
Ответ. 7\sqrt{\frac{29}{5}}
.
Указание. Найдите тригонометрические функции углов DBC
и OBD
и примените теорему косинусов.
Решение. Обозначим AB=CD=x
, AD=BC=y
. Пусть x\lt y
. Из условия задачи следует, что
\syst{x^{2}+y^{2}=100\\xy=48\\}
Из этой системы находим, что x=AB=CD=6
, y=AD=BC=8
.
Пусть точки O
и C
лежат по разные стороны от прямой BD
, а диагонали прямоугольника пересекаются в точке M
. Обозначим
\angle DBC=\alpha,~\angle OBD=\angle ODB=\beta.
Из прямоугольных треугольников BCD
и OMB
находим, что
\sin\alpha=\frac{3}{5},~\cos\alpha=\frac{4}{5},~\sin\beta=\frac{12}{13},~\cos\beta=\frac{5}{13}.
Тогда
\cos\angle CBO=\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta=
=\frac{4}{5}\cdot\frac{5}{13}-\frac{3}{5}\cdot\frac{12}{13}=-\frac{16}{5\cdot13}.
По теореме косинусов
OC^{2}=BC^{2}+BO^{2}-2BC\cdot BO\cos\angle CBO=64+169+2\cdot8\cdot13\cdot\frac{16}{5\cdot13}=
=233+2\cdot8\cdot\frac{16}{5}=\frac{1421}{5}=\frac{49\cdot29}{5}.
Следовательно,
OC=7\sqrt{\frac{29}{5}}.
Сторона OC
треугольника CBO
лежит против тупого угла CBO
(\cos\angle CBO\lt0
). Значит, OC\gt OB\gt OA
. Поэтому OC
— расстояние от точки O
до наиболее удалённой от неё вершины C
прямоугольника.
Аналогично для случая, когда точки O
и C
лежат по одну сторону от прямой BD
.
Источник: Вступительный экзамен на экономический факультет МГУ. — 1979 (отделение политической экономии), вариант 1, № 2H
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 106
