631. В прямоугольный треугольник, периметр которого равен 36, вписана окружность. Гипотенуза делится точкой касания в отношении 2:3
. Найдите стороны треугольника.
Ответ. 9, 12, 15.
Указание. Введите радиус вписанной окружности и воспользуйтесь теоремой Пифагора.
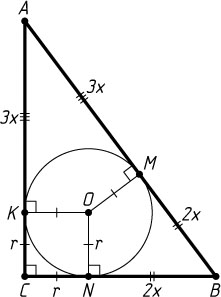
Решение. Пусть M
, N
, и K
— точки касания окружности соответственно с гипотенузой AB
и катетами BC
и AC
треугольника ABC
, O
— центр вписанной окружности, r
— её радиус. Обозначим BM=2x
. Тогда BN=BM=2x
, AK=AM=3x
.
Поскольку CKON
— квадрат, то CN=CK=r
. Поэтому BC=2x+r
, AC=3x+r
. По теореме Пифагора
AB^{2}=BC^{2}+AC^{2},~\mbox{или}~(2x+r)^{2}+(3x+r)^{2}=25x^{2}.
Из этого уравнения находим, что r=x
. Тогда по условию задачи
AB+BC+AC=5x+3x+4x=12x=36.
Следовательно,
x=3,~BC=9,~AC=12,~AB=15.
Источник: Вступительный экзамен на экономический факультет МГУ. — 1980 (отделение политической экономии), вариант 1, № 2
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 107
