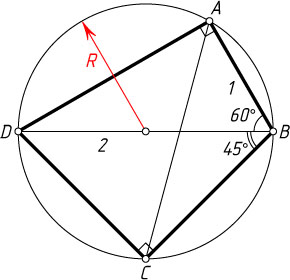
637. Диагональ BD
четырёхугольника ABCD
является диаметром окружности, описанной около этого четырёхугольника. Найдите диагональ AC
, если BD=2
, AB=1
, \angle ABD:\angle DBC=4:3
.
Ответ. \frac{\sqrt{2}+\sqrt{6}}{2}
.
Указание. Треугольник BAD
— прямоугольный.
Решение. Пусть R
— радиус окружности. Поскольку 2R=BD=2
, то
AC=2R\sin\angle ABC=2\sin105^{\circ}=2\sin(60^{\circ}+45^{\circ})=
=2(\sin60^{\circ}\cos45^{\circ}+\cos60^{\circ}\sin45^{\circ})=\frac{\sqrt{2}+\sqrt{6}}{2}.
Источник: Вступительный экзамен на факультет психологии МГУ. — 1978, вариант 1, № 2
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 112
