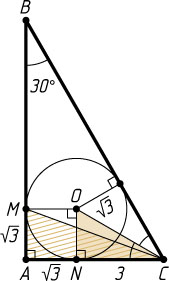
641. В треугольнике ABC
угол A
— прямой, угол B
равен 30^{\circ}
. В треугольник вписана окружность, радиус которой равен \sqrt{3}
. Найдите расстояние от вершины C
до точки касания этой окружности с катетом AB
.
Ответ. \sqrt{15+6\sqrt{3}}
.
Указание. Рассмотрите прямоугольный треугольник MAC
(где M
— точка касания окружности с катетом AB
).
Решение. Пусть O
— центр окружности, r=\sqrt{3}
— её радиус, M
и N
— точки касания с катетами AB
и AC
. Тогда AMON
— квадрат со стороной, равной r
,
\angle OCN=\frac{1}{2}\angle ACB=30^{\circ}.
Из прямоугольного треугольника ONC
находим, что
NC=ON\cos30^{\circ}=r\sqrt{3}=3.
Поэтому
AC=AN+NC=r+3=\sqrt{3}+3.
По теореме Пифагора
CM=\sqrt{AM^{2}+AC^{2}}=\sqrt{3+(\sqrt{3}+3)^{2}}=\sqrt{15+6\sqrt{3}}.
