642. В квадрат ABCD
со стороной a
вписана окружность, которая касается стороны CD
в точке E
. Найдите хорду, соединяющую точки, в которых окружность пересекается с прямой AE
.
Ответ. \frac{2a}{\sqrt{5}}
.
Указание. Примените теорему о касательной и секущей.
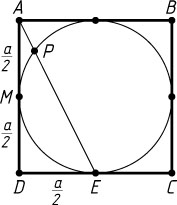
Решение. Пусть PE
— искомая хорда, M
— точка касания окружности со стороной AD
. Тогда
AE=\sqrt{AD^{2}+DE^{2}}=\sqrt{a^{2}+\frac{a^{2}}{4}}=\frac{a\sqrt{5}}{2},~AM=\frac{a}{2}.
По теореме о касательной и секущей
AM^{2}=AE\cdot AP,~\mbox{или}~\frac{a^{2}}{4}=\frac{a\sqrt{5}}{2}\left(\frac{a\sqrt{5}}{2}-PE\right).
Из этого уравнения находим, что
PE=\frac{2a}{\sqrt{5}}.
Источник: Вступительный экзамен на факультет психологии МГУ. — 1980, вариант 2, № 3
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 115
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 12.7, с. 93
