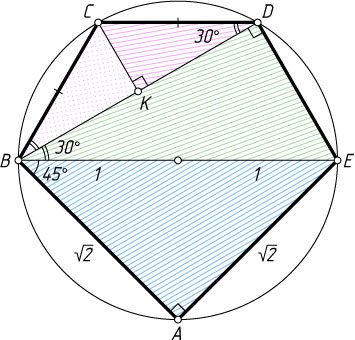
645. Пятиугольник ABCDE
вписан в окружность единичного радиуса. Известно, что AB=\sqrt{2}
, \angle ABE=45^{\circ}
, \angle EBD=30^{\circ}
и BC=CD
. Найдите площадь пятиугольника.
Ответ. 1+\frac{3\sqrt{3}}{4}
.
Указание. BE
— диаметр окружности.
Решение. Пусть R=1
— радиус окружности. Тогда
AE=2R\sin\angle ABE=2\cdot\frac{\sqrt{2}}{2}=\sqrt{2}.
Следовательно, треугольник EAB
— прямоугольный, \angle A=90^{\circ}
. Поэтому BE
— диаметр окружности, BE=2
. Тогда
\angle BDE=90^{\circ},~BD=BE\cos30^{\circ}=\sqrt{3},
\angle DCB=\frac{\cup DAB}{2}=\frac{\cup DE+\cup EAB}{2}=\frac{60^{\circ}+180^{\circ}}{2}=120^{\circ}.
Пусть CK
— высота треугольника DCB
. Тогда
CK=DK\tg\angle BDC=\frac{1}{2}.
Следовательно,
S_{\triangle DCB}=\frac{1}{2}BD\cdot CK=\frac{\sqrt{3}}{4}.
Кроме того,
S_{\triangle ABE}=\frac{1}{2}AB\cdot AE=1,~S_{\triangle BDE}=\frac{1}{2}BD\cdot DE=\frac{\sqrt{3}}{2}.
Поэтому
S_{ABCDE}=S_{\triangle ABE}+S_{\triangle BDE}+S_{\triangle DCB}=1+\frac{\sqrt{3}}{2}+\frac{\sqrt{3}}{4}=1+\frac{3\sqrt{3}}{4}.
Источник: Вступительный экзамен на филологический факультет МГУ. — 1978 (отд. структурной и прикладной лингвистики), вариант 1, № 5
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 122
