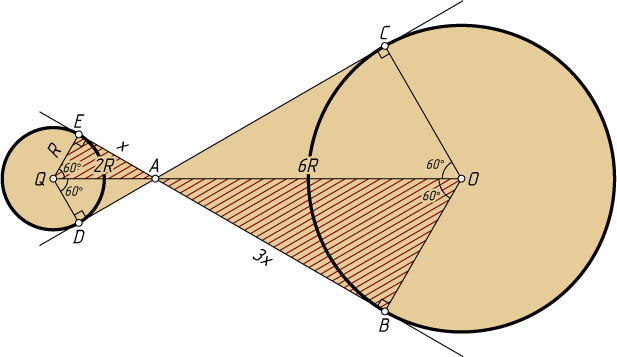
646. Даны две непересекающиеся окружности. К ним проведены общие касательные, которые пересекаются в точке A
отрезка, соединяющего центры окружностей. Радиус меньшей окружности равен R
. Расстояние от точки A
до центра окружности большего радиуса равно 6R
. Точка A
делит отрезок касательной, заключённый между точками касания, в отношении 1:3
. Найдите площадь фигуры, ограниченной отрезками касательных и большими дугами окружностей, соединяющими точки касания.
Ответ. 10R^{2}\left(\sqrt{3}+\frac{2\pi}{3}\right)
.
Указание. Указанные касательные пересекаются под углом 60^{\circ}
.
Решение. Пусть BE
и CD
— общие касательные, B
и C
— точки касания с большей окружностью (с центром O
), D
и E
— с меньшей (с центром Q
).
Из подобия треугольников AEQ
и ABO
следует, что
AQ=\frac{1}{3}AO=\frac{1}{3}\cdot6R=2R.
Поэтому
\angle AQE=\angle AQD=\angle AOC=\angle AOB=60^{\circ},
S_{\triangle AQE}=S_{\triangle AQD}=\frac{R^{2}\sqrt{3}}{2},~S_{\triangle AOB}=S_{\triangle AOC}=\frac{9R^{2}\sqrt{3}}{2}.
Радиусы QD
и QE
разбивают меньший круг на два сектора. Площадь интересующего нас сектора составляет \frac{2}{3}
площади круга, т. е. \frac{2\pi R^{2}}{3}
. Площадь соответствующей части большего круга равна 9\cdot\frac{2\pi R^{2}}{3}
.
Сложив эти площади с найденными площадями треугольников, получим, что искомая площадь равна
S=10\cdot\frac{2\pi R^{2}}{3}+10R^{2}\sqrt{3}=10R^{2}\left(\sqrt{3}+\frac{2\pi}{3}\right).
Источник: Вступительный экзамен на филологический факультет МГУ. — 1979 (отд. структурной и прикладной лингвистики), вариант 1, № 1
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 122
