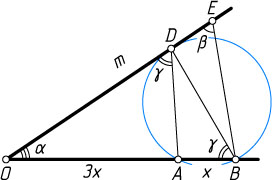
651. На стороне угла с вершиной O
взяты точки A
и B
(A
между O
и B
), причём OA=3AB
. Через точки A
и B
проведена окружность, касающаяся другой стороны угла в точке D
. На луче OD
взята точка E
(D
— между O
и E
). Известно, что OE=m
, \angle BOE=\alpha
, \angle BEO=\beta
. Найдите радиус окружности.
Ответ. \frac{m(7-4\sqrt{3}\cos\alpha)\sin\beta}{8\sin\alpha\sin(\alpha+\beta)}
.
Указание. Примените теорему о касательной и секущей, теоремы синусов и косинусов. Радиус окружности, описанной около треугольника ABD
, найдите по формуле R=\frac{AD}{2\sin\angle ABD}
.
Решение. Обозначим AB=x
, AO=3x
, \angle ODA=\angle OBD=\gamma
, R
— искомый радиус.
По теореме о касательной и секущей
OD^{2}=OB\cdot OA=12x^{2}.
По теореме косинусов
AD^{2}=3x^{2}(7-4\sqrt{3}\cos\alpha).
По теореме синусов
\sin\gamma=\frac{3x\sin\alpha}{AD},~OB=4x=\frac{m\sin\beta}{\sin(\alpha+\beta)},~x=\frac{m\sin\beta}{4\sin(\alpha+\beta)}
Следовательно,
R=\frac{AD}{2\sin\gamma}=\frac{AD}{2\cdot\frac{3x\sin\alpha}{AD}}=\frac{AD^{2}}{6x\sin\alpha}=\frac{3x^{2}(7-4\sqrt{3}\cos\alpha)}{6x\sin\alpha}=\frac{x(7-4\sqrt{3}\cos\alpha)}{2\sin\alpha}=
=\frac{\frac{m\sin\beta}{4\sin(\alpha+\beta)}\cdot(7-4\sqrt{3}\cos\alpha)}{2\sin\alpha}=\frac{m(7-4\sqrt{3}\cos\alpha)\sin\beta}{8\sin\alpha\sin(\alpha+\beta)}.
Источник: Вступительный экзамен на физический факультет МГУ. — 1980, № 5, вариант 2
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1983. — с. 32
