657. В четырёхугольнике ABCD
сторона AB
равна стороне BC
, диагональ AC
равна стороне CD
, а \angle ACB=\angle ACD
. Радиусы окружностей, вписанных в треугольники ACB
и ACD
, относятся как 3:4
. Найдите отношение площадей этих треугольников.
Ответ. 9:14
.
Решение. Обозначим \angle ACB=\angle ACD=\alpha
. Прямые AB
и CD
параллельны, так как \angle BAC=\angle ACB=\angle ACD
, значит, ABCD
— трапеция. Высоты треугольников ABC
и ACD
, проведённые из вершин соответственно C
и A
, равны, поэтому отношение площадей треугольников ABC
и ACD
равно отношению оснований AB
и CD
трапеции.
Центры O
и Q
окружностей, вписанных в треугольники соответственно ABC
и ACD
, — точки пересечения биссектрис этих треугольников, поэтому \angle ACO=\angle ACQ
.
Пусть OM
и QK
— радиусы окружностей, проведённые в точки касания окружностей со стороной AC
, N
— середина основания AD
равнобедренного треугольника ACD
.
Прямоугольные треугольники CKQ
и CMO
подобны по двум углам, причём коэффициент подобия равен \frac{QK}{OM}=\frac{4}{3}
, значит, \frac{CK}{CM}=\frac{4}{3}
.
Положим CK=4x
, CM=3x
. Точка M
— середина основания AC
равнобедренного треугольника ABC
, поэтому
CD=AC=2CM=6x,~AK=AC-CK=6x-4x=2x,~AN=AK=2x,~AD=4x.
По теореме косинусов
\cos\alpha=\frac{AC^{2}+CD^{2}-AD^{2}}{2AC\cdot CD}=\frac{36x^{2}+36x^{2}-16x^{2}}{2\cdot6x\cdot6x}=\frac{7}{9}.
Из прямоугольного треугольника BMC
находим, что
BC=\frac{CM}{\cos\alpha}=\frac{3x}{\frac{7}{9}}=\frac{27x}{7},
значит, AB=BC=\frac{27x}{7}
. Следовательно,
\frac{S_{\triangle ABC}}{S_{\triangle ACD}}=\frac{AB}{CD}=\frac{\frac{27x}{7}}{6x}=\frac{9}{14}.
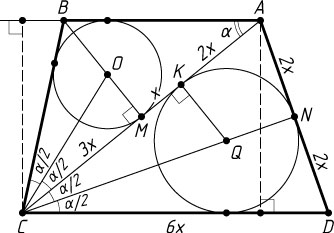
Источник: Вступительный экзамен на биологический факультет МГУ. — 1971, № 5, вариант 2
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 11.33, с. 88
