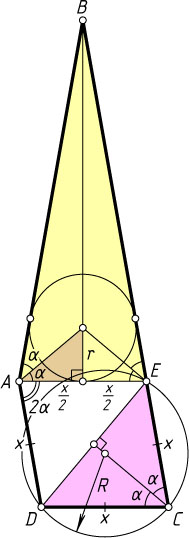
659. Биссектриса AE
угла A
рассекает четырёхугольник ABCD
на равнобедренный треугольник ABE
(AB=BE
) и ромб AECD
. Радиус окружности, описанной около треугольника ECD
, в 1,5 раза больше радиуса окружности, вписанной в треугольник ABE
. Найдите отношение периметров этих треугольников.
Ответ. 3.
Указание. Обозначьте \angle BAE=\angle EAD=\angle ECD=\angle AEB=2\alpha
и составьте уравнение относительно \alpha
.
Решение. Обозначим AE=x
, \angle BAE=2\alpha
. Тогда
DC=EC=x,~\angle EAD=\angle ECD=\angle AEB=2\alpha.
Пусть r
— радиус окружности, вписанной в треугольник ABE
. Тогда r=\frac{x}{2}\cdot\tg\alpha
. Пусть R
— радиус окружности, описанной около треугольника ECD
. Тогда
R=\frac{EC}{2\sin\angle EDC}=\frac{x}{2\sin(90^{\circ}-\alpha)}=\frac{x}{2\cos\alpha}.
По условию задачи
\frac{R}{r}=\frac{3}{2},~\mbox{т. е.}~\frac{x}{2\cos\alpha}=\frac{x}{2}\cdot\tg\alpha\cdot\frac{3}{2}.
Тогда
\tg\alpha\cos\alpha=\frac{2}{3},~\sin\alpha=\frac{2}{3},~\cos\alpha=\frac{\sqrt{5}}{3},~\cos2\alpha=\frac{1}{9}.
В треугольнике ABE
AB=BE=\frac{x}{2\cos2\alpha}=\frac{9x}{2}.
Поэтому его периметр равен \frac{9x}{2}+\frac{9x}{2}+x=10x
.
В треугольнике ECD
DE=2x\sin\alpha=\frac{4x}{3}.
Поэтому его периметр равен x+x+\frac{4x}{3}=\frac{10x}{3}
. Следовательно, отношение периметров равно \frac{10x}{\frac{10x}{3}}=3
.
Источник: Вступительный экзамен на биологический факультет МГУ. — 1971, № 5, вариант 1
