662. A
, B
, C
, D
— последовательные вершины прямоугольника. Окружность проходит через A
и B
и касается стороны CD
в её середине. Через D
проведена прямая, которая касается той же окружности в точке E
, а затем пересекает продолжение стороны AB
в точке K
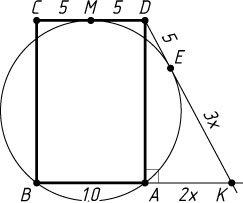
. Найдите площадь трапеции BCDK
, если известно, что AB=10
и KE:KA=3:2
Ответ. 210.
Указание. Примените теорему о касательной и секущей.
Решение. Пусть M
— середина CD
. Тогда DE=DM=5
. Обозначим AK=2x
, KE=3x
. По теореме о касательной и секущей
KE^{2}=BK\cdot AK,~\mbox{или}~9x^{2}=(10+2x)2x.
Из этого уравнения находим, что x=4
. Поэтому
AK=8,~BK=18,~KE=12,~KD=KE+ED=12+5=17.
По теореме Пифагора из треугольника KAD
находим, что
AD=\sqrt{KD^{2}-AK^{2}}=\sqrt{17^{2}-8^{2}}=\sqrt{289-64}=\sqrt{225}=15.
Следовательно,
S_{BCDK}=\frac{1}{2}(BK+CD)\cdot AD=\frac{1}{2}(18+10)\cdot15=210.
Источник: Вступительный экзамен на географический факультет МГУ. — 1969, № 4, вариант 4
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 12.17, с. 94
