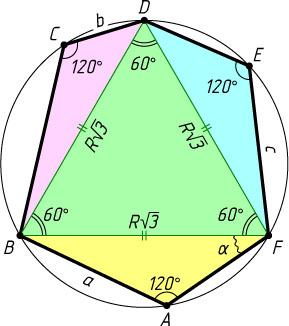
663. В окружность радиуса R
вписан шестиугольник ABCDEF
. Известно, что \angle A=\angle C=\angle E
, AB=a
, CD=b
, EF=c
. Найдите площадь шестиугольника ABCDEF
.
Ответ. \frac{\sqrt{3}}{8}\left(a\sqrt{12R^{2}-3a^{2}}-a^{2}+b\sqrt{12R^{2}-3b^{2}}-b^{2}+c\sqrt{12R^{2}-3c^{2}}-c^{2}\right).
Указание. Треугольник BDF
— равносторонний.
Решение. Пусть R
— радиус окружности. Поскольку \angle A=\angle C=\angle E
, то хорды BF
, BD
и DF
равны между собой. Поэтому треугольник BDF
равносторонний. Следовательно,
\angle A=\angle C=\angle E=120^{\circ},~BF=BD=DF=2R\sin60^{\circ}=R\sqrt{3},
S_{\triangle BDF}=\frac{1}{2}R\sqrt{3}\cdot R\sqrt{3}\sin60^{\circ}=\frac{3R^{2}\sqrt{3}}{4}.
Из треугольника ABF
находим, что
\sin\alpha=\sin\angle AFB=\frac{AB}{2R}=\frac{a}{2R},
\sin\angle ABF=\sin(180^{\circ}-120^{\circ}-\alpha)=\sin(60^{\circ}-\alpha)=
=\sin60^{\circ}\cos\alpha-\cos60^{\circ}\sin\alpha=\frac{1}{2}\left(\sqrt{3(1-\sin^{2}\alpha)}-\sin\alpha\right)=
=\frac{1}{2}\left(\sqrt{3-3\left(\frac{a}{2R}\right)^{2}}-\frac{a}{2R}\right)=\frac{\sqrt{12R^{2}-3a^{2}}-a}{4R}.
Следовательно,
S_{\triangle ABF}=\frac{1}{2}AB\cdot BF\sin\angle ABF=\frac{1}{2}a\cdot R\sqrt{3}\cdot\frac{\sqrt{12R^{2}-3a^{2}}-a}{4R}=
=\frac{\sqrt{3}}{8}(a\sqrt{12R^{2}-3a^{2}}-a^{2}).
Аналогично находим площади треугольников BCD
и DEF
.
Источник: Вступительный экзамен на экономический факультет МГУ. — 1969, № 3, вариант 2
