664. В треугольнике ABC
известно, что AB=20
, AC=24
. Известно также, что вершина C
, центр вписанной в треугольник ABC
окружности и точка пересечения биссектрисы угла A
со стороной BC
лежат на окружности, центр которой лежит на стороне AC
. Найдите радиус описанной около треугольника ABC
окружности.
Ответ. \frac{25}{2}
.
Указание. Выразите углы треугольника через \alpha=\frac{1}{2}\angle ACB
и воспользуйтесь теоремой синусов.
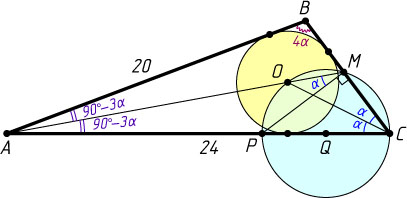
Решение. Пусть O
— центр окружности, вписанной в треугольник ABC
, M
— точка пересечения биссектрисы угла A
со стороной BC
, Q
— центр окружности, проходящей через точки C
, O
и M
, CP
— диаметр этой окружности.
Обозначим \angle OCA=\angle OCB=\alpha
. Тогда
\angle OMP=\angle OCP=\alpha,~\angle AMC=\angle AMP+\angle PMC=\alpha+90^{\circ},
\angle MAC=180^{\circ}-\angle AMC-\angle MCA=180^{\circ}-(\alpha+90^{\circ})-2\alpha=90^{\circ}-3\alpha,
\angle BAC=2\angle MAC=180^{\circ}-6\alpha,
\angle ABC=180^{\circ}-\angle ACB-\angle BAC=180^{\circ}-2\alpha-(180^{\circ}-6\alpha)=4\alpha.
По теореме синусов
\frac{AB}{\sin2\alpha}=\frac{AC}{\sin4\alpha},~\mbox{или}~\frac{20}{\sin2\alpha}=\frac{24}{2\sin2\alpha\cos2\alpha}.
Отсюда находим, что
\cos2\alpha=\frac{12}{20}=\frac{3}{5},~\sin2\alpha=\frac{4}{5}.
Если R
— радиус окружности, описанной около треугольника ABC
, то
R=\frac{AB}{2\sin2\alpha}=\frac{25}{2}.
Источник: Вступительный экзамен на механико-математический факультет МГУ. — 1972, вариант 1, № 3
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 257
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 39, с. 142
